Any list of great contemporary time-wasting activities has to include the FreeCell solitaire card game. Predecessor games go back at least as far as the 1920s. The first computer version of the game was developed by Paul Alfille in 1978 for the Plato educational computer system. The first graphical version of Microsoft FreeCell was written by Jim Horne and was released as part of Microsoft Entertainment Pack 2 in 1992. The game's popularity really began when it was included with Windows 95. Indeed, over the 23 years since then, FreeCell may well be the global champion time-wasting activity.
The popularity of FreeCell is generally credited to the fact that the vast majority of deals – estimates are more than 99.99% – can be solved. The original Microsoft FreeCell contained 32,000 deals identified by number. In 1994 Dave Ring organized the Internet FreeCell Project to verify the claim in Microsoft's help file for the game: "It is believed (though not proven) that every game is winnable." (Current nomenclature uses "deal" where Microsoft said "game" there.) The project was completed in April 1995 with solutions for every deal except number 11982. That deal is now regarded as unsolvable; see below. The Windows XP version of the game provided a million deals, eight of which are regarded as unsolvable. A million is still small; there are a total of 1.75 × 1064 unique deals after accounting for the various ways deals can be transformed by switching column orders or suits in ways that don't affect the solution.
Tournaments were, and still are, organized. Typically these involve being the fastest to solve a particular set of deals. Anything with tournaments is a prime time-waster. Anyone here a fantasy football addict?
The game wastes time, or at least CPU cycles, in other ways. Most people who encounter a deal which is particularly hard to solve eventually ask, "Isn't there a program that could solve this?" FreeCell's simple rules do look to make the game an ideal candidate for brute-force searches for solutions [1]. As it turns out, the solver problem is considerably more difficult than it first appears. These days solvers are readily available and continue to be improved. Deals are generally regarded as unsolvable if none of the automatic solvers can find a solution. The situation only gets worse as soon as people realize that "What's the fewest moves to solve this deal?" is also a thing.
Solvers are not just of interest to amateurs. One of the common problems in artificial intelligence is "planning and scheduling", selecting a sequence of actions to achieve a particular goal. FreeCell has been used as one of the problems in international competitions in the field. A straightforward generalization of FreeCell results in a version of the game which is NP-complete. NP-completeness has been a research topic of interest in theoretical computer science since almost forever. One of the NP-completeness conjectures is a Millennium Prize problem. Answering it one way or the other, with a suitable proof, will win you a million dollars.
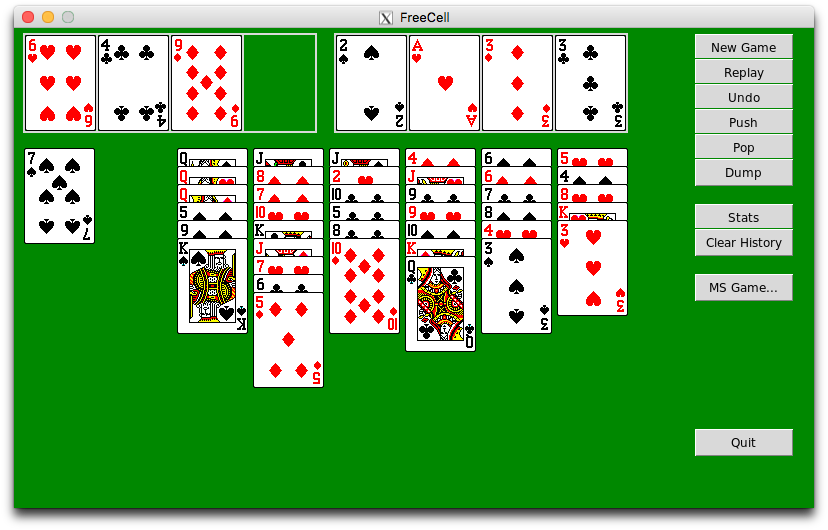
Finally, there are a large number of FreeCell implementations, most of them a waste of the time spent coding them. I should know; I admit that I have written one. At some point I decided that all of the free versions available for the Mac were ugly, or had other undesirable characteristics. I needed a modest project for learning Python, so I wrote a FreeCell program. I still tinker with the code from time to time. Screen shot:

[1] "Clever" search problems are always good for wasting time. My daughter brought this one home from seventh-grade math class years ago. (She was dismayed to discover that her father the applied mathematician said, "Oh, search problems can be soooo cool!")
I stopped at the 7-Eleven store on the way home from work and bought four items. The clerk rang them up and said, "$7.11, please."
"Seems high," I said. "How did you calculate that?"
"I multiplied the four prices together."
"That's not right, you have to add them."
"No problem," he said and punched the numbers in again. "Still $7.11."
What were the prices of the four items?